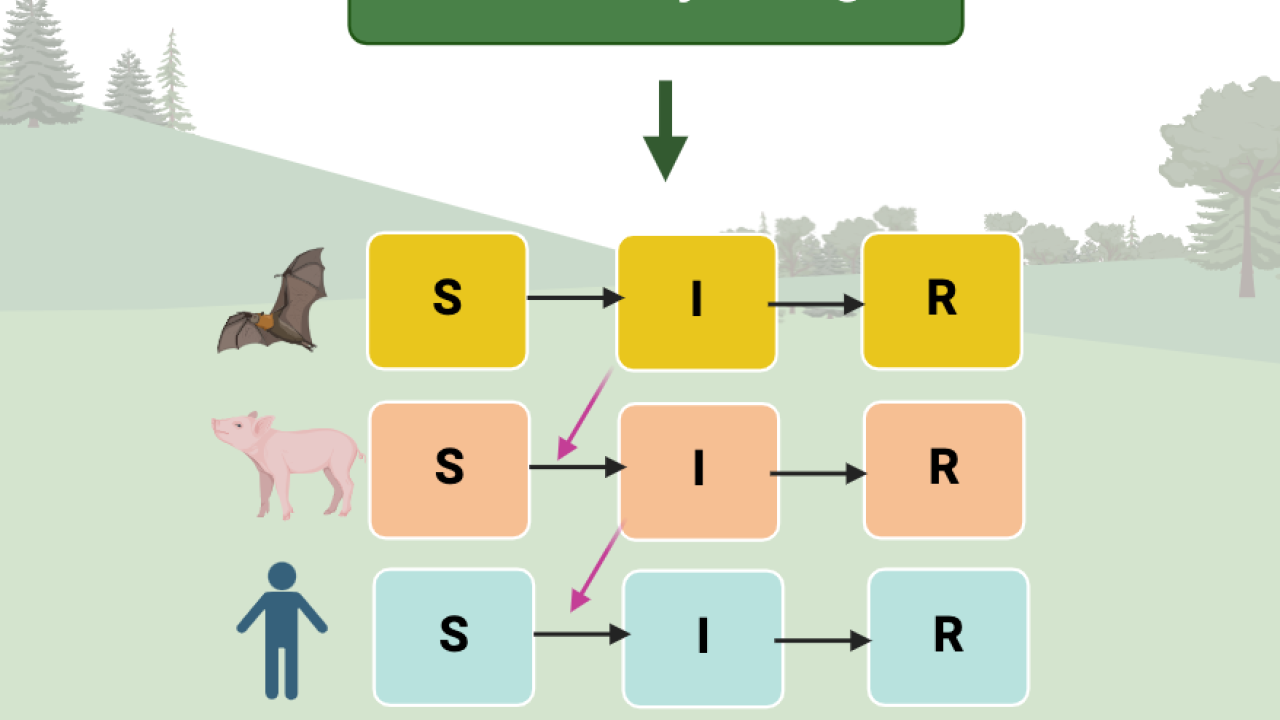
What Models Do (and Don’t) Tell Us About Disease Dynamics

Mathematical models are an important tool that the EpiCenter uses to understand the mechanisms associated with emerging infectious diseases. Although the thought of the many equations involved may be intimidating, the bigger picture is that these models can help to represent the transmission of viruses from one species or individual to another, and how that varies under different, complex conditions. In a dynamic environment affected by climate change and land use alterations, understanding the ways these changes can affect disease intensity and transmission is critical. Modeling is unique in that there are endless possibilities and questions that can be answered, depending on how a model is designed. The model can portray long-term futures, after changes in the environment like landscape modifications such as road building and agricultural development, or it can just represent what we might see over time. While it can be used to make predictions, modeling can also be valuable in understanding interactions that lead to disease transmission and how different factors work together toward an outcome. Models allow us to simplify complex mechanisms in the world in order to gain a better understanding of emerging diseases. The flexibility and freedom in creating mathematical models allows us to create representations of transmission dynamics for various diseases that spread in different ways under different scenarios. 

Modeling also comes with its own set of challenges, as its flexibility can create questions on what parameters should be selected for a model. This inherent uncertainty can be combated in a few different ways. We can validate a model by comparing its predicted outputs to actual observations from previous studies to ensure it is representative of the real world. Another validation method is to borrow ideas and parameters from previous studies. If a virus is similar enough to other viruses that already have real-world data or models on them, we might be able to use these existing parameters. Mathematical modeling used in emerging infectious disease research plays a vital role in identifying the key factors in transmission, which can inform infectious disease interventions, such as controlling mosquito populations, and contribute to management plans for specific diseases. Wildlife disease modeling can be used to identify superhosts or the hosts that contribute the most to the transmission of a particular disease. This knowledge informs decision-making on where resources for prevention or control should be focused. Furthermore, it can help to provide suggestions to reduce disease spread such as educating the public about hygiene measures when working closely with wildlife. Modeling is one aspect of our work that aims to provide science-supported recommendations for policymakers and public health professionals by providing a better understanding of how diseases spread in nature.